Students and Teachers Forum

1. Which transformation does the matrix   0 -1-1   0 represent? Using the matrix, find the image of the point A(6, -2).
 

Here, 0-1-10 represents the reflection in y = -x.  Now,      Object in matrix form = 6-2 and M = 0-1-10 We have,  Image =  M × Object                  = .....

2. What transformation does the matrix 0-1-10 denote? Using the given matrix, find the image of the point A(5, -7).
 

Here, Given transformation matrix = 0-1-10 Let P(x, y) be an object.  Object in matrix form xy      = 0-1-10 × xy    = 0 × x-1 ×y-1 × x+0 × y    = -y-x. Thus, (x, y) .....

3. Find the 2 × 2 matrix which the unit square 01100011 transform to a parallelogram 03410132..
 

Here, given unit square = Object = 01100011 and  Parallelogram = Image = 03410132 Let the required 2 × 2 transformation matrix be M =  abcd. We have,       Transformation matrix × object = Image  So, .....

4. Find the transformation matrix which represents the reflection on the line y = -x. 
 

Let A(x, y) be a point and A'(-y, -x) be the image after reflection on the line y = -x.  So, Object → Image  (x, y) → (y, -x)  or, - y = 0 × x + (-1) × y  or, -x = (-1) × x + 0 × .....

5. Which transformation does the matrix -1001     represent? Find it. 

Here, Given transformation matrix = M = -1001     Let A(x, y) be aobject. We know,         Image = M × object                     = -1001 xy   .....

6. Define the point of inversion.

In a circle with centre O & radius r, if P be the point other then the inverse of P w.r.t. the circle is a point P' on line OP such that OP x OP' = r2, then the image P' is called the inversion pont of .....

7. K(2, 5), L(-1, 3), and M (4, 1) are the vertices of a triangle KLM. Find the coordinates of the images of triangle KLM under the rotation of positive 90°about origin followed by enlargement E [(0, 0), 2]. Present the object and images in the same graph paper.

Here,         Vertices of ∆ KLM are; K(2, 5),  L(-1, 3) and  M (4, 1). We know that,  Object                                 .....

8. State the single transformation equivalent to the combination reflections on the X- axis and Y-axis respectively. Using this single transformation find the coordinates of the vertices of the image of ∆ PQR having vertices P(4,3), Q(1,1), and R(5,-1,). Also, draw the object and image on the same graph.

 Here,          Vertices of triangle PQR are P(4, 3),  Q(1, 1),  and  R(5, -1). We have, Object                               .....

9. The point P(2, -3) is reflected on the X-axis. The image P' thus obtained is rotation through +90° about origin. Find the coordinates of the final image P'' and P'.

Here, We have formula, Object (x, y) Reflection x-axis  -   ———————— .....

10. L (2, 2) O (6, 2) V (7, 4) and E (3, 4) are the vertices of a parallelogram LOVE. Find the co- ordinates of the vertices of the images of parallelogram LOVE under the rotation of positive 90° about origin followed by enlargement E [(0, 0), 3]. Represent the object and images on the same graph paper.

Here,  Given vertices are. L (2, 2), O (6, 2), V (7, 4), E (3, 4) Now, Object                                               .....

11. State the single transformation equivalent to the combination of reflections on the X- axis and Y-axis respectively. Using this single transformation find the coordinates of the vertices of the image of ∆ABC having vertices A(2,3), B(3,4), C(1,-2,) . Also, draw the object and image on the same graph.

 Here,           Vertices of a triangle are A (2,3),  B (3,4),  C (1,-2,). We know that, Object                                 .....

12. C(2, 5), A(-1, 3) and T(4, 1) are  the vertices of the  triangle CAT. Find the coordinates of the images of triangle CAT under the rotation of positive 90° about origin followed by enlargement E [(0,0),  2]. Represent the object and images in the same graph paper.

Here, vertices of ∆ CAT are;           C(2,5) , A(-1,3) and T(4,1). We know that, Object                                     .....

13. Triangle PQR having vertices P(2, 1), Q(5, 3) and R(7, -1) is reflected on the y-axis, the image so formed is enlarged by E[(0, 0),2]. Write the co-ordinates of the vertices of the images thus obtained and present the ∆PQR and its images in the same graph paper. 

.....

14. P(1, 2), Q(2, 1) and R(4, 3) are the vertices of the triangle PQR. Find the coordinates of the images of the triangle PQR under the reflection on the line y = x followed by the enlargement E [(0, 0), 2]. Present the ∆PQR and its images in the same graph paper.

Here, Vertices of ∆PQR; P(1, 2), Q(2, 1) and R(4, 3)     We know that, Object                                             .....

15. Translate the ∆PQR vertices are P (2, 4), Q(-1, 2) and R (5, -1) by translation vector T = - 23 and then reflect the image so obtained in the line x + y = 0. Write the coordinates of the vertices of images and draw the object and images on the same graph paper.

Here,         Vertices of  ∆PQR are; P (2, 4), Q(-1, 2) and R (5, -1). We know that, Object                                     .....

16. The vertices of ∆ABC are A (2, 0), B(3, 1) and C (1, 1). ∆ABC is translated by the vector 2-3 . The image so formed is enlarged by E [(0, 0), 2]. Write the coordinates of the vertices of images thus obtained and represent the object and the images on the same graph paper. 

Here, the vertices of ∆ABC are;  A (2, 0), B(3, 1)  and C (1, 1). We know that, Object                                           .....

17. A  ∆ABC with vertices A(1, 2) B(4, -1) and C(2, 5) is reflected successively in the line y = x and the X- axis. Find the stating
co- ordinates and graphically represent the image under these transformations. State also the single transformation given by the combinations of these transformations.

Here,          Vertices of triangle ABC  are A(1, 2)  B(4, -1)  and  C(2, 5). We know that, Object                               .....

18. In the given figure, ∡RPQ = 90° and S is the mid-point of RQ. Prove by vector method that: PS = QS = RS.

Let, ABC be a right angled triangle whose right angle is at A.  Let, P be the middle point of the hypotenuse BC. Let, A be the origin .....

19.  If a→ = 4, b→ = 5 and a→.  b→ = 10 then find the angle between a→ and b→.  

Here,  a→ = 4,  b→ = 5  and a→. b→ = 10 Let θ be angle between a→ and b→ then,  cos θ = a→. b→ a→b→   = 104 ×5   = 12 or, cos θ  = .....

20. If 3i → + 6j→ and 5i → + 2j → are the position vectors of the points P and Q respectively. Find the position vectors of the point M which divides the line PQ internally in the ratio 3:2. 

Here,  OP → = 3i → + 6j→ and OQ→ = 5i → + 2j→ Ratio = 3 : 2 = m : n. We have,  OM → = mb →+ na → m+n         = 3OQ →+ 2OP .....

21. In the given figure, PQ = PR and QS = RS, then prove by vector method: PS ⊥ QR. 

Let PQR be an isosceles triangle with PQ = QR and PS is median of ∆PQR. PS→ = 12( PQ→ + PR→) [Midpoint theorem] QR→ = (PR→ ) - PQ→) [Triangle law of vector subtraction] PS→. QR→ = 12( PQ→ + PR→)) .....

22. If a→ = 4, b→ = 5 and a→. b  → = 10 then find the angle between a→ and b→.

Here, a→ = 4, b→ = 5. and a→. b→ = 10 Let θ be angle between a→ and b→ then,      cos θ   =  a→. b→ a→b→             .....

23. If p→. q→ = 18√3, p→ = 6 and q→ = 6, find the angle between p→ and q→ .

Here, We have given, p→ . q→ = 18√3 p→ = 6 and q→ = 6, Let θ be angle between p→ and q→ then, cos θ = p→. q→ p→q→ = 1836 ×6 = 3 2 or, cos θ = cos30° or, θ .....

24. If a→ = 4i→ + 2j→ and b→ = -i→ + 2j→, then find the angle between a→ and b→.

Here, a→ = 4i→ + 2j→ and b→ = -i→ + 2j→, So, a→. b→ = (4i→ + 2j→).( -i→ + 2j→)             = -4 + 4 ∴ a→. b→ = 0 If a→. b→ = .....

25. The position vectors of A and B are 9i→ + 7j→ and i→ - 3j→ respectively. If M is the mid-point of AB, find the position vector of M. 

Here,         let O be the origin then,        OA         → = 9i→ + 7j→ And         OB      → = i→ - .....

26. If the position vectors of M and N are 9i→ + 3j→ and 3i→ + 5j→ respectively then find the position vector of a point P such that MP→ = PN→.

Here,  Let O be the centre OM→ = 9i→ + 3j→ And ON→ = 3i→ + 5j→ We have given,         MP→ = PN→ or, OP→ - OM→ = ON→ - OP→ or, 2OP→ = OM→ + .....

27. The position vector of A and B are 2i→ + 7j→ and 7i→ - 3j→. Find the position vector of a point which divides AB internally in the ratio of 2:3. 

Here,     let O be the origin then,      OA→ = 2i→ + 7j→ and OB→ = 7i→ + j→      And the given ratio = m:n                  .....

28. If the position of the midpoint of the line segment EF is 4i→ + 7j→ and the position vector of a point E is -i→ - 4j→, find the position vector of the point F. 

Here, let O be the origin and P be the mid-point of EF. So,  OP→ = 4i→ + 7j→ OE→ = -3i→ - 4j→ Since P is the mid-point of EF.                 So, OP→ = OE →+ .....

29. If 10i→ - 7j→ and i→ + 10j→ are perpendicular to each other find the value of a. 

Here,   Given perpendicular vectors are:     10i→ - 7j→ &  ai→ + 10j→ . Using the condition of perpendicularity     (10i→ - 7j→). (ai→ + 10j→) = .....

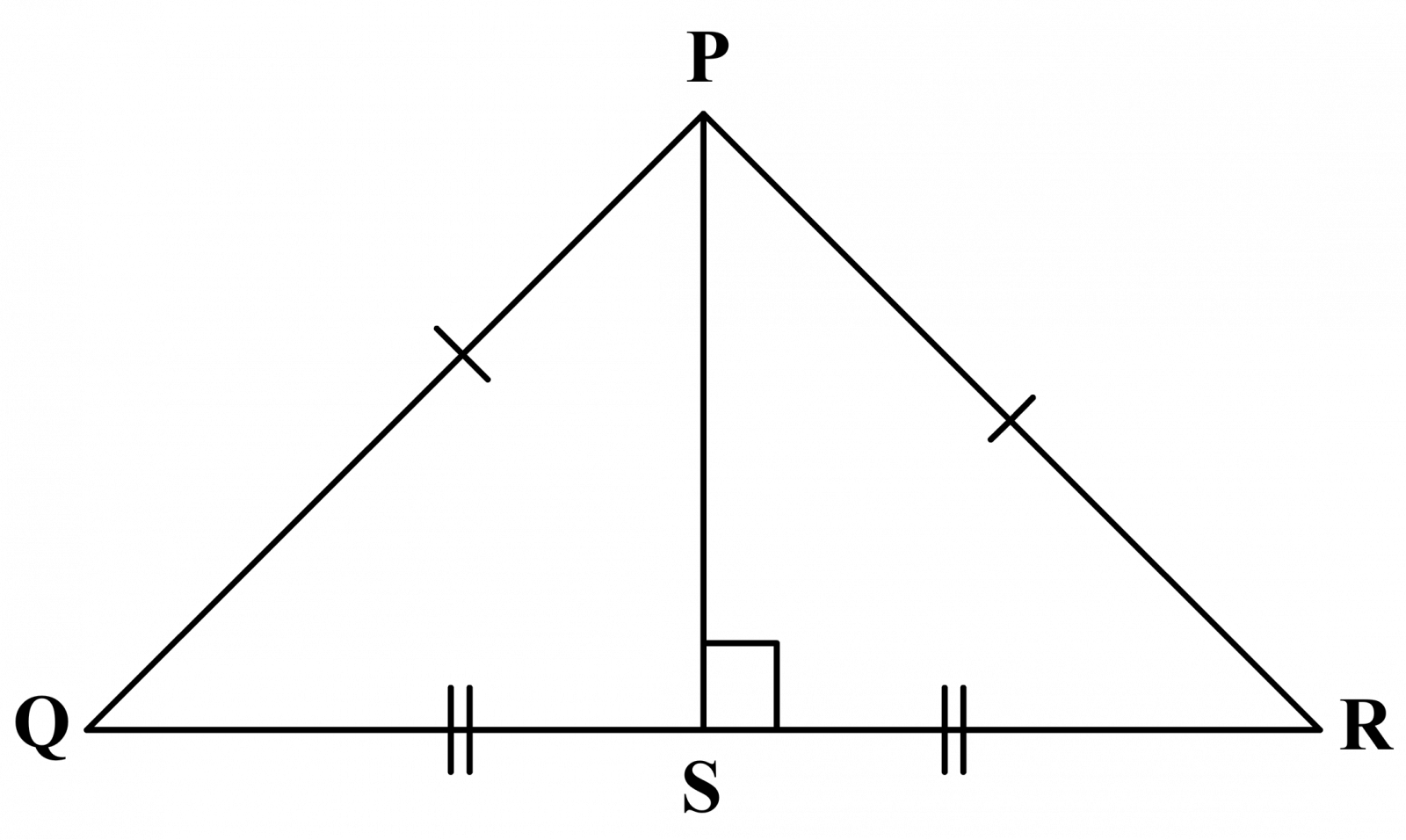
30. Prove by vector method that the line joining the mid-point of the base and the vertex of an isosceles triangle is perpendicular to the base.

Let PQR be an isosceles triangle with PQ = PR and PS is median of ∆PQR. (i) PS→ = 12(PQ→ + PR→)[Mid-point theorem] (ii)QR→ = (PR→ - PQ→)[Triangle law of vector subtraction] (iii)

31. If a→ = 5√3, b→ = 6, and θ = 30°, find the value of a→ . b→.

Here, a→ = 5√3, b→ = 6, and θ = 30°. We know that, cos θ = a→. b→ 53 ×6 or, 3 2 = a→. b→ 53 ×6 or, a→. b→ = 45 Thus, the value of a→. b→ is .....

32. If the position vectors of the vertices A, B and C of ∆ABC are (3i→ + 5j→), (5i→ - j→) and (i→ + 8j→) respectively, find the position vectors of the centroid G of the triangle. 

Let O be the origin then, OA→ = 3i→ + 5j→ OB→ = 5i→ - j→ OC→ = i→ + 8j→ . Let G be the centroid then,  OG→ = 13(OA→ + OB→ + OC→)        = 13(3i→ + .....

33. If p→ + q→ + r→ = 0, p→ = 6, q→ = 7 and r→ = √127, find the angle between p→ and q→.

Here, p→ + q→ + r→ = 0,.................(i) p→ = 6, q→ = 7 and r→ = √127 Now,       p      → + q→ = -r→                [ .....

34. In the figure, if PA → = 14PQ →,
Prove that a → = 14(3p→ + q→): 

Here,  PA → = 14PQ → (By the triangle law of vector subtraction.) or, OA → - OP → = 14(OQ → - OP →) or, a → - p → = 14(q → - p →) or, 4a → - 4p → = q → - p → or, 4a → = .....

35. If OA→ = a→ , OB→ = b→ and the point M divides the line segment AB internally in the ratio of m1:m2, then prove that:
       OM       →  =  m1b→+ m2a→ m1+ m2

Let O be the origin OA→ = a→ , OB→ = b→ and M be a point on AB which divides AB in the ratio of m1:m2. From the figure, AMMB = m1 m2 or, AM→ MB→ = m1 m2 or, m2(OM→ - OA→ ) = m1(OB→ - OM→ ) or, .....

36. Prove vectorically that the diagonals of a rectangle are equal.

Here, Let ABCD be a rectangle and  AC and BD are its diagonals. (i) AC2 = (AC→)2 = (AB→ + BC→)2 = (DC→ + BC→)2 [∴ AB = DC]       = DC→2 + 2DC→. BC→ + BC→2    .....

37. If p→  = 2i - 2j & q→  = 4j , what is the value of p→ .q→ ?

Here,  p→  = 2i - 2j & q→  = 4j = 0i + 4j , Now,  p→ .q→ = 2⨯0 + (-2)(4)                       = - .....

38. If a→  = (3, 0) & b→  = (4, -3), what is the value of a→ .b→ ?

Here,  a→  = (3, 0) & b→  = (4, -3), Now,  a→ .b→ = (3, 0).(4, -3)                       = 3⨯4 + 0(-3)         .....

39. If j→  is unit vector along the y-axis, what is the value of j2→ ?

We know,  j→  = (0, 1). So, j2 = → j→ .j→  = (0, 1).(0, 1) = 0 + 1 = .....

40. If i→  be the unit vector along the x-axis, what is the value of i→ 2 ?

We know,  a→  = (1, 0). So, i2 = → i→ .i→  = (1, 0).(1, 0) = 1 + 0 = .....

41. If a→  = (2, 0) & b→  = (0, 4), what is the value of a→ .b→ ?

Here,  a→ . b→ = (2, 0).(0, 4)                = 2 x 0 + 0 x 4              = 0 + 0              = .....

42. If the position vectors of two points A and B are 32 and –52 respectively then find position vector of the mid-point C of AB. 

Let O be the origin then, OA→ = 32 and OB→ = -54 Let C be the mid-point of AB.  Then,  OC→ = 12(OA→ + OB→)       = 1232+ -54       = 123-52+4       = 12-26   .....

43. If a→.b→=0, what is the angles between vectors a→&b→?

If a→.b→=0, then the angle between a→&b→ is .....

44. If a→.b→= |a|→|b|→, what is the angle between a→&b→?

The angle between a→&b →is 0o or .....

45. In the given figure, PQ = QR and RS = SP, then prove by vector method: PR ⊥ QS.

Here, Given PQ = QR = RS = SP To prove: PR ⊥ QS Proof: 1.  PR→ = PS→ + SR→[Triangle law of vector addition]    2. QS       → = QP→ + PS→[Triangle law of vector .....

46. If a→ + 2b→ and 5a→ - 4b→ are perpendicular to each other and a→ and b→ are unit vectors, find the angle between a→ and b→.

Here, a→ and b→ are unit vectors, so a→ = and b→ = 1 Since, (a→ + 2b→) and (5a→ - 4b→) are perpendicular to each other. So, (a→ + 2b→). (5a→ – 4b→) = 0 or, 5a2 - 4a→. b→ + .....

47. If a→ = -5i→ + 3j→ and b→ = pi→ + (p + 2) j→ are perpendicular to each other, find the value of p.

Here, a→ = -5i→ + 3j→ and b→ = pi→ + (p + 2) j→ Since, a→ ⊥ b→, So a→ . b→ = 0 i.e. (-5i→ + 3j→) . [pi→ + (p + 2) j→] = 0 or, - 5 × p + 3 (p + 2 ) = 0 or, -5p + 3p + .....

48. If b→ = 6, a→. b→ = 12 and angle between a→ and b→ (θ ) = 60°, find the value of a→.

Here, b→ = 6, a→. b→ = 12 and θ = 60°, We know that, cos θ = a→. b→ a→b→ cos60° = 12a→ ×6 12 = 2a→ Thus, the value of a→ is .....

49. If the position vectors of two points A and B are 34 and 45 respectively then find the position vector of the mid-point K of AB.

Here,  Let O be the origin then,  OA→ = 34 And OB→ = 45 We know that,  OK→ = OA→+ OB→2       = 1234+ 45       = 123+44+5       = 1279       = .....

50. In the given parallelogram SR→ = 4i→ - 2j→ and PR→ = 6i→ + 5j→, find QR→.

Here,         SR          → = 4i→ - 2j→ and PR→ = 6i→ + 5j→ . We know that,  QR→ = PS→ = PR→ + RS→       = 6i→ + .....