Students and Teachers Forum

1. The area of a triangle is equal to the area of one half of the area of a parallelograms standing on the same base and between the same parallels.

Given:∆ABE and //gm ABCD are on the same base AB and between the same parallels AB and DE. To prove:∆ABE = ½ of //gm ABCD in area Construction:From A, draw AF // BE meeting DF and .....

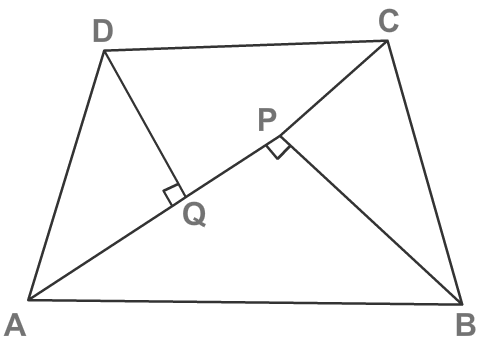
2. ABCD is a parallelogram and P, any point inside it. AP, BP, CP and DP are joined. Prove that: ∆APB + ∆CPD = ∆APD + ∆BPC.

Given: ABCD is a parallelogram and P is any point inside it. AP, BP, CP and DP are joined.   To prove:  ∆APB + ∆CPD = ∆APD + ∆BPC  Construction: Draw EPF ⊥ DC and AB & draw GPH ⊥ BC and .....

3. ABCD is a parallelogram. P is any point on the diagonal BD. Prove that ∆APD = ∆CPD.

Given: ABCD is a trapezium. P is any point on diagonal BD. To prove:  ∆APD  = ∆CPD Construction: Draw EPF //BC//AD and GPH//AB//DC.  Proof:  Statements Reasons  1.  ∆ADB = ∆BCD ∆DGP = .....

4. ABCD is a rhombus in which BC measures 8 cm. If DE is perpendicular to AB and measures 3 cm, find the area of the rhombus ABCD.

Given,            Base of rhombus (AB) = (BC) = 8 cm           Altitude (DE) = 3 cm. We know, Area of the rhombus (A) = base (AB) ⨉ height (DE)             .....

5. Prove that the area of a triangle is one half the area of a parallelogram standing on the same base and between the same parallels.
 

Given:              Para. ABCD and ∡ABE are standing on same base AB and between same parallels AB//DC. To prove:            Area of Para. ABCD = 12 of Area of .....

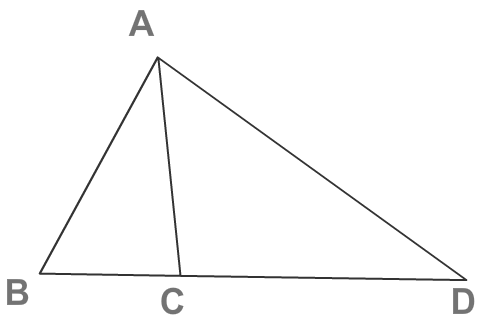
6. What divides a triangle into two equal halves?

The median of a triangle divides a triangle into two equal .....

7. ABCD is a trapezium with AB//DC, E and F are the points on BD and AC respectively such that EF//AB or DC. Prove that
(i) ∆AOE = ∆BOF in area. 
(ii) ∆ACE = ∆BDF in area.

Given:           ABCD is a trapezium with AB//DC. E and F are the points on BD and AC respectively such that EF//AB or DC.  To prove:            ∆AOE = ∆BOF in area .     .....

8. In the figure, if AB//CD, prove that the area of parallelogram ABCD and area of parm. EBCF are equal to each other.

 

Given:            Parm. ABCD and Parm. BCEF are standing on same base BC and between same parallels AF//BC. To prove:           Area of Parm. ABCD = Area of Parm. .....

9. Prove that the parallelograms on the same base and between the same parallels are equal in area.

 

Given:            Parallelogram ABCD and parallelogram ABEF are in standing on the same base AB and between the same            parallels line FC//AB. To Prove:       .....

10. Prove that the area of △PXY is equal to half of the area of the parallelogram WXYZ standing on the same base XY and between the same parallel lines WP and XY.

Given:              Para. WXYZ and △PXY are standing on same base XY and between same parallels WP//XY. To prove:             Area of Para. WXYZ = 1/2 of Area of .....

11. ABCD is a parallelogram with area 48 sq. cm. If the altitude DM on the side AB is 6 cm and the altitude DN on the side BC is 8 cm, find the adjacent sides of the parallelogram.  

Solution: Given,                 Area of parm. ABCD = 48 cm2                 Altitude of DM on side AB (h1) = 6 cm               .....

12. The base of a parallelogram whose area is 24 cm2 is 6 cm. Find its altitude.
 

Given,        Base of the parallelogram (b) = 6 cm        Area of the parallelogram (A) = 24 cm2 We know,            Area of a parallelogram (A) = base (b) ⨉ altitude .....

13. ABCD is a trapezium. DF is perpendicular to BC. If AD = 5.6 cm, BC = 6.4 cm and DF = 4 cm, find the area of the trapezium ABCD.

Given,               Length of parallel sides,               BC= 6.4 cm and (AD) = 5.6 cm               Distance between the two parallels (DE) .....

14. ABCD is a square and ABEC, a parallelogram on the same base AB and between the same parallels AB and DE. If AD = 8 cm, find the area of the parallelogram. Also find the area of the triangle ABE.

Given, AD = 8 cm So, base (AB) = AD = 8 cm  (measure of the sides of a square being equal) We know, Area of square (A) = l2             = (8 cm)2            .....

15. Parallelogram ABCD and a triangle ABE are on the same base AB and between the same parallels AB and DE. If the area of the  ∆ABE = 7 cm2, find the area of the parallelogram ABCD.
 

Given,              Area of ∆ABE = 7 cm2              Area of parallelogram ABCD     = 2 ∆ABE                  .....

16. Triangles on the equal bases and between the same parallels are equal in area.

Given:          ∆ABC and DEF are on the equal bases BC and EF respectively and between the same parallels AD and BF. To prove:          ∆ABC = ∆DEF in area. Construction:       .....

17. In the given figure, ABCD is a quadrilateral and DB∥CE. Prove that: Area of quadrilateral ABCD = Area of ∆ADE.
 

Here, Given: DB ∥ CE                                                     To prove: Area of quadrilateral ABCD = Area .....

18. In parallelogram ABCD, E is any point on AB. DE and CB are produced to meet at F. If CE and BD are joined,
Prove that ∆BDF = ∆CEF.

Given:           ABCD is a parallelogram. E is any point on AB and DE and CB are produced to meet at F. CE and BD are joined. To prove:             ∆BDF = ∆CEF .....

19. Prove that the triangle PQR triangle SQR standing on the same base QR and between the same parallels PS and QR are equal in area.

Given:           ∡PQR and ∡SQR are standing on same base QR and between same parallels PS//QR. To prove:            Area of ∡PQR = Area of ∡SQR. Construction: From point P, draw PX .....

20. PQRS is a parallelogram in which the altitude SM on the side PQ is 9 cm, and its area is 45 sq. cm. Find the base of the parallelogram.

We have, Area of parallelogram PQRS = height of parallelogram × base of parallelogram      Or, 45cm2 = 9cm ⨉ base       Or, base = .....

21. What is the relation between area of parallelogram and rectangle standing on same base and between same parallels? Write it.

The area of parallelogram and rectangle standing on same base and between same parallels are .....

22. ABCD is a trapezium. DF is perpendicular to BC. If AD = 8 cm, BC = 12 cm and DF = 6 cm, find the area of the trapezium ABCD.

Given, Length of parallel sides, (AD) = 8 cm and (BC) = 12 cm Distance between the two parallels (DF) = 6 cm We know, Area of a trapezium (A)             = ½ (sum of parallel sides) ⨉ distance between the .....

23. ABCD is a parallelogram such that AB is 7 cm. If DM is perpendicular to AB and DM is 4 cm, find the area of the parallelogram ABCD.

Given,         Base (AB) = 7 cm         Distance between the parallels (DM) = 4 cm. We know, Area of a parallelogram (A) = base (AB) ⨉ height (DM)                 .....

24. The diagonal of a parallelogram bisect it into .......... parts.

The diagonal of a parallelogram bisect it into ...2....... .....

25. Prove that parallelograms on the same base and between same parallel lines are equal in area.

Given: Parallelograms ABCD and EBCF are standing on the same base and between same parallel lines .....

26.
In the given figure, area of ∆ADE = 40 cm2, ABCD is a rectangle, BC = 10 cm, find the length of AB.

i. Area of ABCD = 2 Area of ∆ADE      [∵Area of parallelogram is double of area of triangle standing on same base and between same parallel lines]                       .....

27.
In the given figure PQ = QR = RS = PS, QS = 10 cm and area of ∆PQT = 22.5 cm2. Find the length of PR.

i. Area of rhombus PQRS = 2 Area of ∆PQT [∵Area of parallelogram is double of area of triangle standing on same base and between same parallel lines]                           .....

28.
In the given figure, BCFE is a parallelogram and ABCD is a square. If the area of parallelogram is BCFE = 200 cm2, find the length of AC.

i. Area of square ABCD = Area of parallelogram BCFE [∵ Area of parallelograms on the same base and parallel lines are equal and a square can be taken as parallelogram]               .....

29.
In the given figure, ABCD is a parallelogram. AF ⊥ BC, AE ⊥ CD, AF = 8cm, BC = 10cm, and AE = 5cm, find the length of CD.

i. Area of parallelogram ABCD = AE.CD. ii. Area of parallelogram ABCD = AF.BC. iii. From i and ii, we get            AE.CD = AF.BC        or, 5 cm × CD = 8 cm × 10 cm     .....

30.
Prove that: Area of ∆PSN = Area of ∆MQR.

Given: PQ ∥ MN ∥ SR To prove: Area of ∆PSN = Area of ∆MQR. Proof: S.N Statements: S.N Reasons: 1 ∆PMN = ∆QMN 1 Triangles on the same base and between same parallel lines are equal in .....

31.
In the given figure, ABCD is a parallelogram. X is any point within it. Prove that the sum of ∆XCD and XAB is equal to half of the area of ABCD.
 

Given: ABCD is a parallelogram and X is a point within it. To prove: Area of ∆ XCD + XAB = parallelogram  ABCD ⨉ 1/2  Construction: PQ ∥ AB and CD is drawn through .....

32.
In the adjoining figure, PQRS and LQMN are two parallelogram of equal area. Prove that: LR ∥ SN

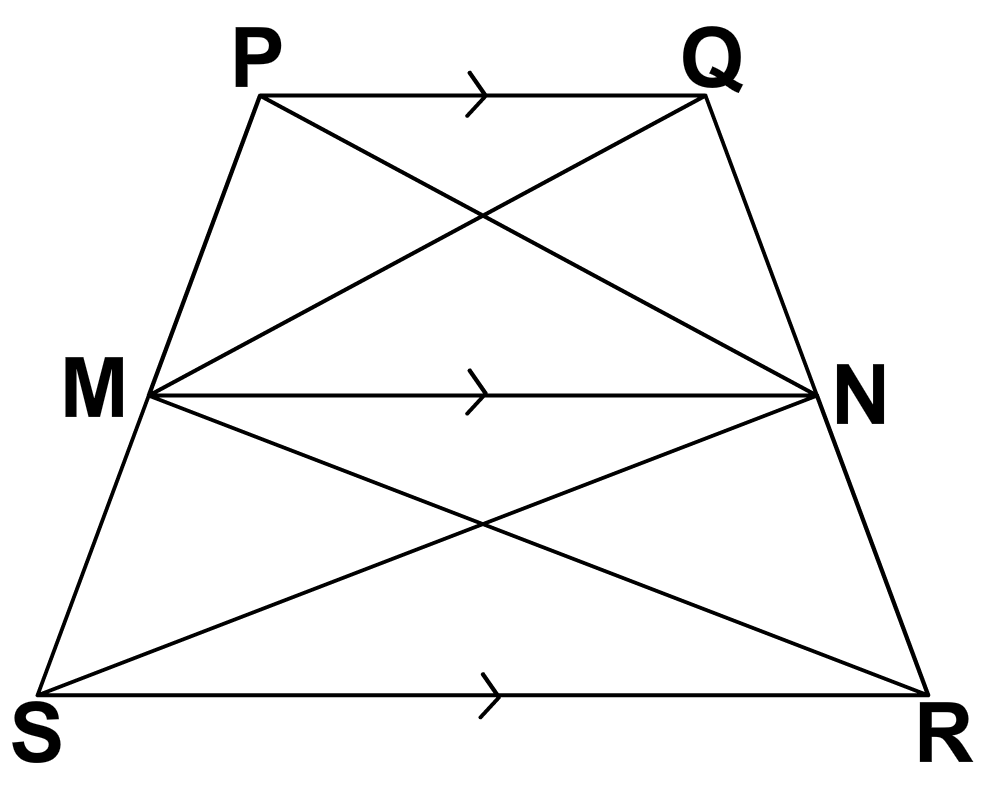
Given:          Area of parallelogram PQRS is equal to area of parallelogram LQMN. To prove:           LR ∥SN Construction:            L is joined with S and R is .....

33.

In the given figure Q and R are mid-points of AC and AB respectively. P is any point on BC.
Prove that: Area of ∆PQR = 1/4  Area of ∆ABC
 

Given: Q and R are mid-points of AC and AB respectively. To prove: Area of ∆PQR = 1/4  Area of ∆ABC  Construction: B & Q are joined. Proof: S.N .....

34.
In the given figure ABCD is a square, the length of whose diagonal AC is 6cm. Find the area of ∆ADE.

i. Area of square ABCD  = 12 AC2                                           = 12(6cm)2              .....

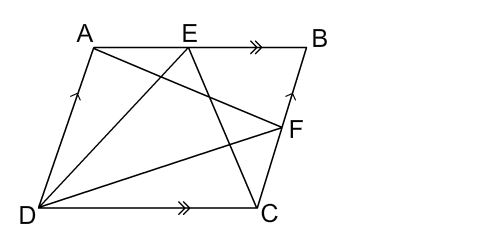
35. ABCD is a parallelogram and E is any point on AB. DE and CB are produced to meet at F. Prove ∆AEF = ∆BCE in area.

Given:            ABCD is a parallelogram and E is any point on AB. DE and CB are produced to meet at P.            AF and CE are joined. To prove:           .....

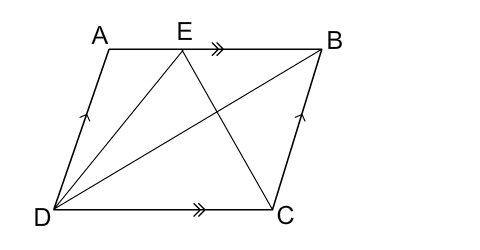
36. ABCD is a quadrilateral. AB is produced to any point E such that CE joined is parallel to DB. DE is joined.
Prove that quadrilateral ABCD = ∆ADE.

Given:         ABCD is a quadrilateral. AB is produced to E such that CE joined is parallel to DB. DE is joined. To prove:         quadrilateral ABCD = ∆ADE. Construction:Join .....

37. Find the area of the shaded region in the given plane figures.
ABCD is a parallelogram; O is any point on AB and DOC is a triangle; AOB produced to M such that CM is 8 cm; DC = 10 cm, triangles ADO and COB are shaded.

Given,           Base of parallelogram (DC) = 10 cm           Distance between the parallels sides (h) = 8 cm. Now,  Area of parallelogram ABCD = base (DC) ⨉ height (h)    .....

38. Find the sum of areas of Triangle CED and CBD.
ABCD is a parallelogram. E is a point on AB. DE, DB and CE are drawn.EF drawn perpendicular to DC is 6 cm. AB is 8 cm. Triangle CED and CBD are shaded.

Given,          Base of parallelogram ABCD (DC) = (AB) = 8 cm          Height of parallelogram ABCD (EF) = 6 cm. We know,  Area of parallelogram ABCD (A)  =  base (AB) ⨉ height .....

39. Find the sum of areas of triangles AFD and CED.

ABCD is a parallelogram. F is a point on BC and E is a point on AB. Triangle AFD and triangle CED are shaded.AD = 12 cm and FG perpendicular to AD is 8 cm.)
 

Given,        Base of parallelogram ABCD (AD) = 12 cm        Height of parallelogram ABCD (FG) = 8 cm. We know,  Area of parallelogram ABCD (A) = base (AD) ⨉ height (FG)         .....

40. Find the area of the shaded region in the given plane figures.

Parallelogram ABCD such that AC is the diagonal. AE is drawn perpendicular to BC. BC = 12 cm and AE = 9 cm. Triangle ADC is shaded

Given,         Base of parallelogram ABCD (BC) = 12 cm         Height of parallelogram ABCD (AE) = 9 cm. We know, Area of parallelogram ABCD = base (BC) ⨉ height (AE)        .....

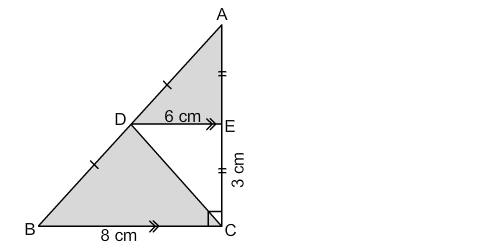
41. Find the area of the shaded region in the given plane figures.

triangle ABC such that AC is perpendicular to BC. D is a mid-point on AB and E is a mid-point on AC such that DE is parallel to BC. BC =8 cm, EC = 3 cm, DE = 6 cm; Triangle BDC and ADE is shaded.

Given, Base of triangle BEC (BC) = 8 cm Height of triangle BEC (EC) = 3 cm We know, Area of triangle BEC (A) = ½ ⨉ base (BC) ⨉ height (EC)                 = ½⨉8 cm ⨉3 .....

42. In the given figure, AB//DC//EF, AD//BE and AF//DE. Prove that parallelograms. DEFH = ABCD in area.

 

Given: AB//DC//EF, AD//BE and AF//DE.  To prove:  Parm. DEFH = Parm. ABCD in area Proof:  Statements Reasons 1.parallelograms. DEFH = parallelograms. DEGA 2.parallelograms. ABCD = parallelograms. .....

43. In the figure, AE||BC, square ABCD and ∆EBC are standing on the same base BC between the same parallels. If AC=6 cm, find the area of ∆EBC.

Area of ∆EBC = 12 × area of square ABCD                         =12 × (12×AC2)                         .....

44. In the adjoining figure, D is the midpoint of side AC. If 2DE=BC=12cm, then find the area of ∆ABC.

Here, Construct a line BD. Given,     2DE=BC=12cm ==> DE = 6cm  &  BC= 12cm. Area of triangle BDC = 12 × DE × BC                           .....

45.
In the given figure, ABCD is a parallelogram. The area of ∆DMN = 15 cm2, what is the area of ∆BCN?

i. Area of ∆ADM = 1/2 Area of parallelogram ABCD         [∵ Area of triangle is half of area of parallelogram standing on same base and between same parallel lines] ii. Area of ∆ABN =  1/2         .....

46. In the given figure, ABCD is a parallelogram of area 20cm2. What is the area of the shaded part?

Given, Area of //gm = 20cm2 Now, Area of Tr. ABE = 12  ⨉ Area of //gm = 10cm2. Area of shaded region  = Area of //gm ABCD - Area of Tr.ABE                           .....

47. In the adjoining figure, MP=6cm and PR=8cm. Calculate the area of ∆MNQ.

Area of ∆MNQ = 12×Area of para. MNOP                           = 12×MP×PR                       .....

48. In the given figure, ABCD is quadrilateral. If AC = 10cm, BP = 8cm and DQ = 4cm, what is the area of the quadrilateral?

Given: AC = 10cm, BP = 8cm and DQ = 4cm Area of qd.ABCD = ? We know, Area of qd. ABCD = 12 AC ( BP + QD)                                = 12 ⨉ 10cm ( 8cm + .....

49. Find the area of the given quadrilateral ABCD where AM and CN are perpendiculars to BD and 4AM=2CN=BD=12 cm.

Given,                4AM = 2CN = BD = 12 cm                =>  AM=3 cm, CN=6 cm and BD=12 cm. Now, Area of the quad. ABCD = 12 × BD(AM+CN)    .....

50. In the given figure, the area of ∆ABC = 15cm2, 2BC = CD. What is the area of the ∆ABD?

Here, ∆ABC = 15cm2, 2BC = CD. ∆ABD= ∆ABC  + ∆AC D            = 15cm2 + 2 ⨉15cm2         [ Since,  2BC = CD.] .....