Given:             ABCD and PQRD are two parallelograms.                                      .....

Here,             Base of parallelogram ABCD (AD) = 8 cm          Height of parallelogram ABCD (AF) = 6 cm. We know,  Area of a parallelogram (ABCD) =  base (AD) ⨉ height .....

Here, Construct a line MX perpendicular to PR. Now,         MX = NR = 10cm. In right angled ∆MPX, PX = MP2-MX2       = 102-82       = 6 cm. Here, area of the quad. MNRP = 72 .....

Given:           Parallelograms ABCD and EBCF are on the same base BC and between the same parallels AF and BC.  To prove:            Parallelogram ABCD = Parallelogram .....

       Let us join B with C. i. Area of ∥gram     = 2 × Area of ∆DBC (∵ The diagonal divides a parallelogram into two equal parts)           .....

i. Area of ∆BCF = Area of ∆BEF [∵ Median divides a triangle into two equal parts]                            = 24 cm2 ii. Area of parallelogram ABCD = 2 Area of ∆BCF [∵ .....

Let us join D with F. i. Area of square ABCD = AB2                                         = (6cm)2             .....

Given, Base of parallelogram ABCD (BC) = 15 cm Height of the parallelogram ABCD (DF) = 10 cm. We know, Area of parallelogram ABCD (A) = base (BC) ⨉ height (DF)                 = 15 cm⨉ .....

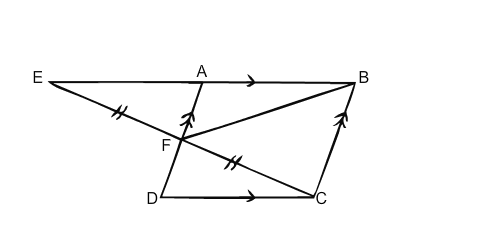
Given:            ABCD is a parallelogram. E and F are points on AB and BC respectively. To prove:             (i) ∆AFD = ∆DEC             (ii) .....

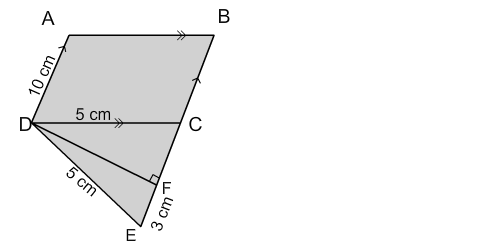
In right angled triangle ADC,              DC=√(AC2 - AD2 ) = √(5.32 - 52 ) = 1.76cm. For triangle ABC, s = 12(5.3 + 3.2 + 6) = 7.25 cm. Now, area of triangle ABC .....

Given, the area of the para. ABCD =24 cm2. a.    Area of ∆EAB = 12 × area of para. ABCD                                = 12 × .....

Given,         Area of parallelogram (A) = 32 cm2         Base of the parallelogram (b) = 8 cm. We know, Area of parallelogram (A) = base (b) ⨉  height (h) or, 32 cm2 = 8 cm ⨉ h or, h = 4 cm. So, .....

Given:           ABCD is a trapezium and AB//MN // DC. To prove:             ∆AND  = ∆BMC . Proof:   Statements  Reasons  ∆ANM = .....

Given:           Here, ABCD is a parallelogram. To prove:            Area of ∆APQ = Area of ∆PDC . Proof:   Statement Reason

Here, a = 6cm Area = √34  ⨉a2          =  .....

Given,        Area of triangle (A) = 56 cm2        Altitude of the triangle (h) = 8 cm. We know, Area of a triangle (A) = ½ ⨉ base (b) ⨉ altitude (h) Or, 56 cm2 = ½⨉ b ⨉ 8 cm Or, 56 cm2 .....

The area of parallelogram ABCD= 2 × the area of triangle AEB = 2× 24 = 48 .....

Given:         In ∆ABC, two medians BE and CD intersect at O.          BD = DA, AE = EC  To prove:          Area of ∆BOC = Area of quadrilateral ADOE Construction:   .....

Given: ABCD is a parallelogram and AM = ME To prove: Area of ∆ABE = Area of parallelogram ABCD. Construction: M and B are joined. Proof: S.N .....

Given,              Base of parallelogram ABCD (AD) = 10 cm. Using Pythagoras theorem,  Height of parallelogram  = Height of triangle (DF)                  .....

Here,               Area of ∆DEC=Area of Trap. ABCD-Area of para. ADEB            = Area of Trap. ABCD - 2 × Area of ∆ADC            = 100-2 .....

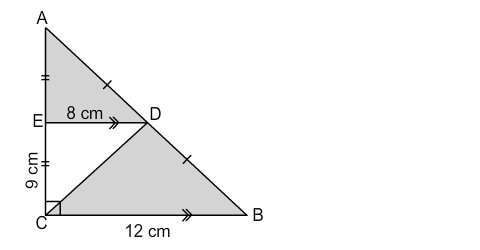
Given, Base of triangle BEC (BC) = 12 cm Height of triangle BEC (EC) = 9 cm We know, Area of triangle BEC (A)  =  ½ ⨉ base (BC) ⨉ height (EC)                         .....

The area of rhombus is equal to two times the area of triangle standing on same base and between same parallel .....

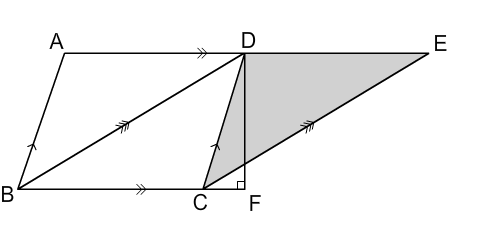
Given:        Rectangle ABCD and Parallelogram EBCF are standing on the same base and between .....

i. Area of ∆ADC = 2 Area of ∆DEC [Median divides the triangle into two equal parts]                             = 2 × 10 cm2             .....

The area of triangle ADC = (1/2)× the area of parallelogram ABED = 12 ×100 = 50 .....

Given: ABCD is a parallelogram and P is any point on the diagonal AC. To prove: Area of ∆ABP = Area of ∆APD. Construction: B is joined with D and Q be the point of intersection of AC & .....

Given :             In ∆ABC, DE//BC             BE and CD are joined. BE and CD meet at O. To prove :            ∆BOD = ∆COE in area. Proof .....

The area of parallelogram AQRB = the area of parallelogram PQRS = 64 .....

    In right angled ∆AEF, AE = AF2-EF2        = AF2-CF-CE2        = 132-28-232        = 12 cm.     Now, the area of the trapezium ABCF = .....

The area of quadrilateral ABCD is given by, Area = 12 ⨉ d(p1+p2)         = 12 .....

Given: D, E and F are mid-points of BC, AD and AB respectively To prove: ∆ABC = 8∆EFG Construction: B and E are joined. Proof:

.....

Area of rhombus ABCD = ½×AC×BD                                         = 0.5×20×28           .....

Let x be the greater  and y  be the smaller  numbers. Then, from the first condition, x+y=5………1) From the second condition, x-y=1………2). Adding equation 1 and 2, we get, x + y = 5  x- y .....

Let the age of son at 2032 be x. Therefore, the age of his father in 2032 = 4x. At 2050,          Age of sun = x + 18         And, age of father = 4x + 18, From question,       4x + 18 = .....

Let the length of the room be ‘x’ and breadth be ‘y’. So,     xy  = 45…(i) From given condition, Since after subtracting 3m length and adding 1 m to breadth makes it a square,     .....

Let, x be the number. Then,  or,   x2-3 = 6  or,   x2 = 3+6  or,   x  = ±√9 = ±3. ∴ x = ±3 are the required .....

Let, x be the required number. Then,  x-2= 8x  or,x2-2x+8 = 0 Or, x2-4x+2x-8 = 0 Or,x(x-4)+2(x-4) = 0 Or, (x+2)(x-4) = 0 Either, x = -2       Or, x = 4. Since, x is whole number, x = 4. Hence, the required number is .....

Let, a number be a.  Then,       6a+11=65  Or, 6a=54  Or, a=9. Therefore, the required number is .....

Let,  a and (a+1) be two consecutive numbers. Then,        a + (a+1)=25 or,   2a   =24 ∴     a =12 And, a+1=12+1=13. Hence, the required numbers are 12 and .....

Let, x be the number. Then,      2x2 = 6x or, x2 = 3x or, x2-3x = 0 or, x(x-3) = 0 Either,  x = 0     Or, x-3 = 0    Or, x = 3. ∴ x = 0 or 3. Hence, required no. .....

Let the age of the son be x and father’s age be y. So,   13(x -1 ) = y - 1 or, y = 13( x - 1) + 1  ….(i) And,     x3 = y ….(ii) So, using (i),    x3 = 13(x – 1) + 1 or, x3 – 13x + 12 = .....

Let, a be the required natural number. Then, according to question  or, 2a = a2  or, a = 2 [a≠0}. Hence, the required number is .....

The difference between the father and the son is always constant. Hence, The difference between the father and the son after 18 years = 21 .....

Let, x be the required number. Then,      x2/2-4 = 14   or, x2 = 36  ∴   x = √36          = 6. Hence, the required number is .....

Let, x be the number. Then, according to question,              x2 = 5         or, x = 2⨉5         or, x = 10. Therefore, the no. is .....

Let, R and S be the number of marbles that Ram and Sita possesses initially. Then, from the first case,       R – 1 = S + 1  Or, R =S + 2 ……….i). Again, from the second case,     R + 1 = 2( .....

Let, w, x, y and z be the present ages of A, B, C and D respectively. Now, by the question,    w – x = 2 …………..1)    z = 2w ……………….2)    x = .....

Let the numerator of fraction be ‘x’. Therefore the denominator of the fraction is ‘x -1’. So, the fraction becomes: x/ (x+1). From the given condition, Or, (x + 1)/ ( x + 6) = 1/2 Or, 2(x + 1) = x+ 6 Or,2x + 2 = x + 6 Or, .....

Let, x and (x+2) be the two consecutive even numbers. Then,        (x+2)2-(x)2 = 20 Or, x2+ 4x+4 - x2 = 20 Or, 4x = 16  ∴    x = 4. Hence, the required smaller number is .....