Students and Teachers Forum
|
C.I. |
20 – 30 |
30 – 40 |
40 – 50 |
50 – 60 |
60 – 70 |
|
Frequency |
8 |
a |
5 |
4 |
3 |
Here, First quartile (Q1) = 30.625, so Q1 class = 30 – 40. Cumulative frequency table of given data is given .....
|
C.I. |
0 – 5 |
5 – 10 |
10 – 15 |
15 – 20 |
20 – 25 |
|
f |
6 |
4 |
7 |
5 |
8 |
The maximum marks obtained by below 75% students = Q3. Cumulative frequency table of given data is given by:
We have given, = a and ∑fx=b, Number of terms (N) = ? We have, .....
Given ∑fx = 370 + 20a, ∑f = 23 + a and = 17. a = ? We have, Mean () = ∑fx∑f = 370+20a23+a Or, 17 = 370+20a23+a Or, 391 + 17a = 370 + 20a Or, 21 = 3a or, a = .....
Given, = 50 and ∑ fx = 750, Number of terms (N)= ? We have, = ∑fxN or, 50=750N ∴N=75050=15, which is required .....
| Daily wages (Rs.) | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 |
|---|---|---|---|---|---|
| No. of workers | 3 | 4 | 12 | 8 | 5 |
Find the median.
Here, Daily wages (Rs.) No. of workers (f) Cumulative frequency (cf) 30-40 3 3 40-50 4 7 50-60 12 19 60-70 8 27 70-80 5 32 N = .....
Given, First quartile class = 20- 30 and if (N4 - c.f) =8, We have given, The first quartile of the given series is given by, .....
Given, First quartile class = 20- 30 and if (N4 - c.f) =8. The first quartile of the given series is given by, First quartile = L + if (N4 - .....
Given, Third quartile class = 40 – 50 and if (3N4 - c.f)=4. The third quartile of the given series is given by, Q3 = L + if (3N4 - .....
Given, = 15, N = 32 and ∑fx = 350+13p, p = ? We have, = ΣfxN or, 15 = 350+13p 32 or, 350+13p = 32×15 or, 13p .....
In the given curve, sum of frequencies (N) = 20. We have, Third quartile class = (3N4 )th item = (34 ⨉ 20)th item .....
We have given, In a continuous series, the value of assumed mean is a and the sum of frequencies (f) is N &the deviation is (d), .....
In the given curve, sum of frequencies (N) = 30. We have, median class = (N2 )th item = (302)th item .....
Given, Mean () = 12, ∑fx = 70 + 10a and the number of frequency (N) = 5 + a, a = ? We have, Mean () = ∑fxN = 70+10a5+a Or, 12 = 70+10a5+a Or, .....
Given, = 50, ∑fx = 750, Number of terms (N) = ? We have, = ∑fxN or, 50=750N ∴ N=75050=15, which is required .....
In the given curve, sum of frequencies (N) = 20. We have, First quartile class =( N4)th item = (20 4)th item .....
Given, =32, N = 15 and ∑fx = k, k = ?. We have, = Σfx .....
Solution: The sample space when two dice are thrown is:
1st dice/ .....
When a coin is tossed two times, the probability of getting head in 1st toss P(H) = 12 And the probability of getting head on 2nd toss is P(H) = 12 ∴ The probability of getting both head when a coin is tossed is .....
| Outcomes | 1 | 2 | 3 | 4 | 5 | 6 |
| Frequency | 186 | 205 | 211 | 187 | 204 | 207 |
Calculate the empirical probability of
i. less than 4
ii. greater than 3
iii. even numbers
iv. less than or equal to 3.
Here, Total no. of trails n(S) = 1200 i. Let E1 be the event of getting faces less than 4. Then n(E1) = 186 + 205 + 211 .....
Let, G, Y and B denote the events of getting a ball of green, a ball of yellow and a ball of blue respectively. Then, the tree diagram is as shown in .....
Let, W and B denote the events of getting a ball of white and a ball of black respectively. Then, the tree diagram is as shown in figure. Now, from the tree diagram, We have, probability of getting same colours= P(BB) + P(WW) = .....
Here, The probability of solving a problem by student X, P(X) = 80 % = 0.8 The probability of solving a problem by student Y, P (Y) = 75% = 0.75. Now, The .....
Here, Sample space(S) = {1, 2, 3, 4, 5, 6} ∴n(S) = 6. Now, probability of getting 1, 3 or 5 is given .....
Let, H and T denote the events of getting a head and a tail respectively. Then, the tree diagram is as shown in figure. Then from the diagram, probability that both are tails = P(TT) = .....
Let, S = son and D = daughter. This is the case of independent event. Probability of a son, P(S) = 12 Probability of a daughter, P(D) = 12. Tree-diagram: Sample space: .....
Let, W = white ball, B = blue ball and G = green ball Then, n(W) = 3, n(B) = 4 and n(G) = 5 This is the case of dependent event. Tree-diagram: From the tree diagram, P(both are same color) = P(WW) or .....
For cards; Total no. of cards n(S) = 52 . Let E1 be the event of getting king, then n(E1) = 4. ∴ Probability of getting king cards P(E1) = 452 .....
No. of head = n(H) = 1 No. of tail = n(T)= 1. Tree diagram: Outcomes: Probability: (H, H, H ) P(H, H, H) = 1/2 × 1/2 × 1/2 = 1/8 .....
Here, No. of red ball = 1 No. of blue ball = 1 No. of white ball = 1. The Probability of getting one ball of each colour is: P(R, B, W) + .....
Let A and B be the event that the 1st and 2nd person hit the target. Now, P(A) = 34 P(A)ˈ = 1 - 34 = 14. .....
Let, B = black pen, Y = yellow pen and W = white pen Then, n(B) = 5, n(Y) = 3 and n(W) = 2 Probability of an ace card, P(A) = 452 Probability of a non-face card, P(N) = 4852. Tree-diagram: From the diagram, a) Both are blue = .....
Given, The probability that A can solve a problem is 15 . We know, Probability that A can not solve = P(A') = 1 - P(A) .....
Let, W = white ball, B = blue ball and G = green ball Then, n(W) = 1, n(B) = 1 and n(G) = 1 This is the case of dependent event. Tree-diagram: Sample space = {GB, GW, BG, BW, WG, .....
Let, B = black balls and W = white balls. Then, n(R) = 6 and n(W) = 3. Tree-diagram: This is the case of dependent event. a) From the tree diagram, P(both white) = P(WW) .....
Let, B = blue balls, Y = yellow balls and W = white balls. Then, n(B) = 5, n(Y) = 3 and n(W) = 2. Probability of an ace card, P(A) = 452 Probability of a non-face card, P(N) = .....
Let A = ace cards and N = non-ace cards Then, n(A) = 4 and n(N) = 48 Tree-diagram: This is the case of dependent event. From the tree diagram, P(both aces) = P(AA) = 452 X 351 .....
Let, G = green and B = blue Then, n(G) = 6 and n(B) = 3 This is the case of dependent event. Probability of a green ball, P(G) = 69 Probability of a blue ball, P(B) = 39 Tree-diagram: a) Sample space: {BB, BG, GG, GB}. b) Probability .....
Solution: Let, R = red balls and W = white balls. Then, n(R) = 3 and n(W) = 2. Tree-diagram: This is the case of independent event. Probability of a red ball, P(R) = 35 Probability of a white ball, P(W) = 25 From the tree .....
Let, G and B denote the events of giving birth to a girl and a boy respectively. Then, the tree diagram is as shown in figure. From the diagram, probability that all are girls= P(GGG) = .....
Let, B and G denote the events of selecting a boy and a girl respectively. Then, the probabilities are shown in tree diagram. Possible outcomes = { GG, GB, BG, .....
Let , B = blue and R = red Then, n(B) = 8 and n(R) = 4 This is the case of dependent event. Probability of a blue ball, P(B) = 812 Probability of a red ball, P(R) = 412 Tree-diagram: a) Probability that both balls are blue, P(BB) = P(B) .....
Here, for a dice, Sample space, S1 = {1, 2, 3, 4, 5, 6}. For a coin, Sample space, S2 = {Head, tail}. Now, probability of getting 3 on the dice and head on the coin is .....
Let ,W = white and G = green Then, n(W) = 3 and n(G) = 6 This is the case of dependent event. Probability of a white ball, P(W) = 39 Probability of a green ball, P(G) = 69 Tree-diagram: a) Probability that one is white and the .....
Let A be the event of king cards and B be the events of black cards. Then, Number of king cards n(A) = 4 Number of black cards n(B) = 26 Number of .....
Let A and B be the set of balls numbered with multiple of 4 and 5 respectively. Then, S = {1, 2, ........., 20} A = {4, 8, 12, 16, 20} B = {5, 10, .....
Let A and B be the set of cards divisible by 4 and 7 respectively. Then, S = {2, 3, 4, ..........., 25} A = {4, 8, 12, 16, 20, 24} B = {7, 14, .....
Given, Number of yellow balls = 5 Number of blue balls = 3 Number of green balls = 2 Total number of balls = 5 + 3 + .....
Given, No. of face cards = 12 No. of non face cards = 40 Total no. cards = 52. Let E be the event of getting face cards and Eˈ be the event of .....
Let A and B are sets of prime number and cube number cards respectively. ∴ S = {6, 7, 8, ............, 39} A = {7, 11, 13, 17, 19, 23, 29, 31, 37} .....
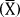 = a and ∑fx=b, find the number of terms (N).
= a and ∑fx=b, find the number of terms (N)..png) = 17, find the value of a.
= 17, find the value of a..png) = 50 and
= 50 and .png) = 15, N = 32 and ∑fx = 350+13p, find the value of p.
= 15, N = 32 and ∑fx = 350+13p, find the value of p..png)
.png) of the data.
of the data..png)
.png) ) = 12, ∑fx = 70 + 10a and the number of frequency (N) = 5 + a, find the value of a.
) = 12, ∑fx = 70 + 10a and the number of frequency (N) = 5 + a, find the value of a..png) = 50 and ∑fx = 750, find the number of terms (N).
= 50 and ∑fx = 750, find the number of terms (N)..png)
.png) =32, N = 15 and ∑fx = k, find the value of k.
=32, N = 15 and ∑fx = k, find the value of k.