Let K be the events of getting king cards and N be the events of getting non-king cards.  Then,       Number of king cards n(K) = 4        Number of non-king cards n(N) = 48        Total .....

Solution: Let R, W and B be the event of getting red, white and blue balls respectively.      No. of red balls, n(R) = 5      No. of white balls, n(W) = 7      No. of blue balls, n(B) = 10     .....

 Let E be that Nepal does not wins a football match. ∴ P(E) = 23      P(E)ˈ = 1 - 23                =  13. The Probability that Nepal lose all the three matches .....

Here,       No. of white balls = 6       No. of black balls = 5       Total no. of balls = 6 + 5                               .....

Let, B = black pen, Y = yellow pen and W = white pen Then,          n(B) = 5, n(Y) = 3 and n(W) = 2.         Probability of an ace card, P(A) = 452         Probability of a non-face .....

Let, B = black  andW = white Then, n(B) = 3 and n(W) = 2 Probability of a white ball, P(B) = 35 Probability of a green ball, P(W) = 25 Tree-diagram: This is the case of dependent event. a) Probability that both balls are of same color, .....

           Let, R and B denote the events of getting a ball of red and a ball of blue respectively.            Then, the tree diagram is as shown in .....

Let, B = boys  and G = girls Then, n(B) = 1 and n(G) = 1 Tree-diagram: This is the case of independent event. Probability of a boy, P(B) = 12 Probability of a girl, P(G) = 12 a) Sample space: {BB, BG, GG, GB}. b) Probability that both .....

Let , H = head and T = tail. Tree-diagram: This is the case of independent event. Probability of a head, P(H) = 12 Probability of a tail, P(T) = 12 Sample space : {HH, HT, TH, .....

Let , B = black pen, Y = yellow pen and W = white pen. Then, n(B) = 1, n(Y) = 1 and n(W) = 1. Tree-diagram: This is the case of dependent events. From the tree diagram, P(first white pen) = P(WB) or P(WY)            .....

Here, Sample space, S = {7, 8, 9, 10,….., 27} Set of prime numbers, A = {7, 11, 13, 17, 19, 23} Set of even numbers, B = {8, 10, 12, 14, 16, 18, 20, 22, 24, 26} The probability of getting a prime or even is given by,       .....

Let H and T be the event of getting head and tail respectively.  Tree-diagram: Here, Outcomes             Probabilities  (H, H)                   .....

Here,       Total number of cards, n(S)=52        Number of kings, n(K) = 4        Number of aces, n(A) = 4. Now, probability of the getting a king or an ace is given by,    P(K or .....

Let, B = black balls and W = white balls. Then, n(B) = 5 and n(W) = 3 This is the case of independent event. Probability of a black ball, P(B) = 58 Probability of a white ball, P(W) = 38 . Tree-diagram: From the tree diagram, P(both black) .....

For a Dice,       S1 = { 1,2,3,4,5,6}   ∴  n(S1) = 6. Even numbered face = E = { 2,4,6}    ∴ n(E) = 3. For a Coin,     S2 = { H,T}  ∴ n(S2) = 2     n(H) = .....

Possible days = S = { Sunday, Monday, Tuesday, wednesday, Thursday, Friday, Saturday} ∴ n(S) = 7. E = Sunday ∴n(E) = 1. So,  Probability that the exam on Sunday = n(E)n(S)                 .....

Total no. of cards = n(S) = 52 No. of non-face card = n(F') = 40. We know, Probability of getting a non-face card = P(F') = n(F')n(S)                             .....

Table for outcomes: Possible outcomes = S = { HH,HT,TH,TT} ∴ n(S) = 4. Outcomes with at least one head = H= { HH,HT,TH} ∴ n(H) = 3. Probability of getting at least one head = P(H) = n(H)n(S)         .....

In a leap year total number of days is 366. So, there are 52 weeks and 2 days.  These two days may be:     { Sunday & Monday, Monday & Tuesday, Tuesday & Wednesday, Wednesday & Thursday, Thursday & Friday, Friday .....

Let, B = black pen, Y = yellow pen and W = white pen Then, n(B) = 1, n(Y) = 1 and n(W) = 1 This is the case of dependent events. Tree-diagram: From the tree diagram, P(first white pen)                .....

Let A and B be the events of yellow and green balls.           Number of yellow balls n(A) = 4           Number of green balls n(B) = 8           Total number .....

Let A be the event of getting 5 on dice and B be the event of not getting 5 on dice.  Then,        n(A) = 1       n(B) = 5       n(S) = 6. Tree-diagram; Outcomes    .....

The set of all the possible outcomes of an experiment is called sample space of the experiment. Example: Sample space when a fair coin is tossed is        S = {H, T} . The sample space when a dice is thrown is    .....

Two events A and B are said to be mutually exclusive events, if their simultaneous occurrence is not possible.   For example, let S = {1, 2, 3, 4, 5, 6}                           .....

Here, Possible outcomes = 2 So, probability of absent = .....

0 ≤ P(E) ≤ .....

The probability of sure events is .....

Let B be the events of being boys and G be the events of being girls.  Then,         n(B) = 1,        n(G) = 1,        n(S) = 2. Tree-diagram: Outcomes    .....

Let, R and W denote the events of getting a ball of red and a ball of white respectively. Then, the tree diagram is as shown in figure. From tree diagram, we have,        Probability of getting both red = P(RR)= .....

Let, Y, R and B denote the events of getting a ball of yellow, a ball of red and a ball of black respectively. Then, the tree diagram is as shown in figure. Now, Sample space = {(R,Y),(R,B),(Y,R), .....

We have given,            A and B are two mutually exclusive events .            P(A) = 13 and P(B) = 14. So,       P(A ∪ B) = P(A) + P(B)     .....

Probability of solving by A, P(A) = 13 . ∴ Probability that A cannot solve P(A)ˈ = 1 - 13                                       .....

Given:            P(A)ˈ = 56            P(A) = 1 - 56   =  16              .....

Here, P (Q) = 35 P(R)= 15, And two events Q and R are mutually exclusive events. i) P (Q ∪ R) = P(Q) + P(R)= 35 + 15 = 45 ii) P (Q∪R)ˈ = 1 - P(Q ∪ R) =1 – 45  = .....

Here,  The probability of solving a problem by student A, P(A) = 13  The probability of solving a problem by student B, P (B) = 14. Now,  The probability of not solving a problem by student A, P(A)ˈ = 1 - 13 = 23 The .....

Here,        Sample space(S) = {2, 3, 4, 5, ……, 33}        Set of squared number (A) = {4, 9, 16, 25}        Set of cubed number (B) = {8, 27}. Now, the probability of .....

Given,        A and B are two independent events,          P(A) =  13 and P(B) = 14 . We know,         P(A&B) = P(A) . P(B)           .....

Let , G = green cap, B = blue cap and W = white cap.         Then, n(G) = 1, n(B) = 1 and n(W) = 1. Tree-diagram:        This is the case of dependent event. Sample space = {GB, GW, BG, BW, WG, .....

a) Given:                         P(A) = 0.38                        P(B) = 0.16             .....

Let, B = boys  and G = girls Then, n(B) = 20 and n(G) = 30. Tree-diagram: This is the case of independent event. Probability of a boy, P(B) = 2050 Probability of a girl, P(G) = 3050 Sample space: {BB, BG, GG, .....

Given: Let A and B be the events of getting 5 on the first dice and even number on the 2nd dice respectively.  For the 1st dice        n(A) = 1        n(S) = 6 . ∴ Probability of getting 5 on 1st .....

Let, K and K denote the events of getting a king and not getting a king from well-shuffled deck of cards respectively. Then, the tree diagram is as shown in figure. From the tree diagram,          We have, probability of .....

Let, B and W denote the events of getting a ball of black and a ball of white respectively. Then, the tree diagram is as shown in figure. From the diagram,        Probability of getting both white balls= P(WW) = .....

Solution:  Probability of selection of A, P(A) = 16 ∴ Probability of not selection of A, P(A)ˈ = 1 - 16                                      .....

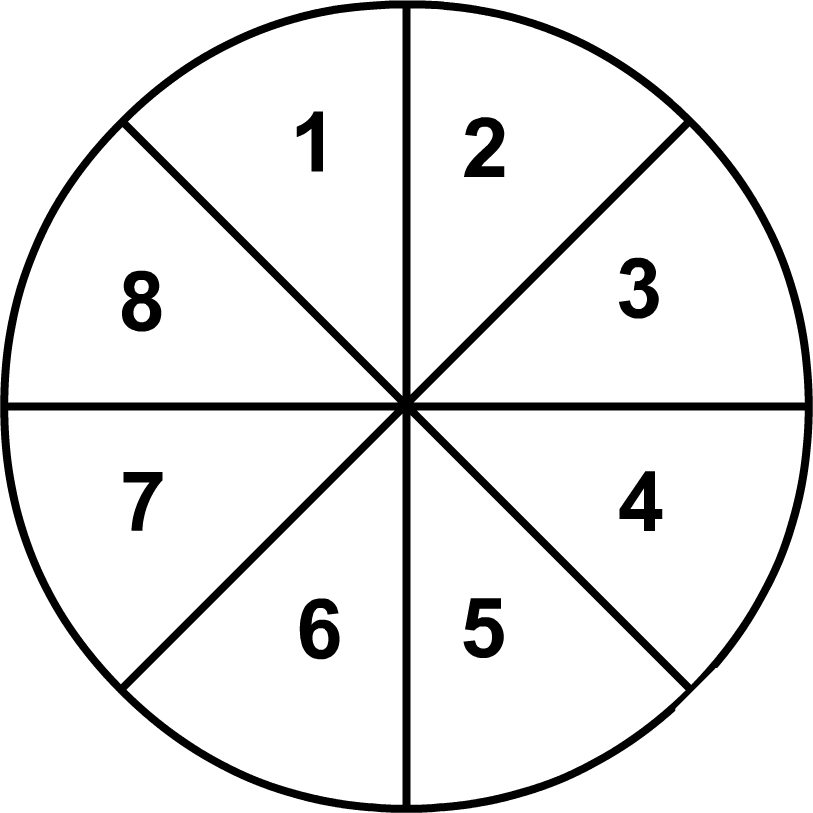
Here. Total no. of sectors (n) = 8 i. The Probability of the pointer to stop on either 4 or 6 is: (P) = 28                                      .....

  Area of square =    12 .....

Here, d1 = 10cm d2 = 12cm. Area of Rhombus = 12 ⨉ d1 ⨉ d2                              = 12⨉ 10cm ⨉ 12cm           .....

Given: Rectangle ABCD and parallelogram ABEF are on the same base and between the same parallels AB and DE. To prove: //gm ABEF = Rect. ABCD in area Proof:  Statements Reasons  In triangles ADF and BCE    .....

Given:           In ∆ABC, AD is the median. To prove:           ∆ABD = ∆ACD in area. Construction:           From A, draw EAF // .....

Here, p1 + p2 = 15cm h = 6cm Area  = 12 ⨉ h(p1 + p2 )           = 12  ⨉ 6cm  ⨉ 15cm           =  .....